Why Resistance Noise

Introductory courses on noise in electronic circuits often start by stating the following formula for the open-circuit noise voltage of a resistor:

In formula 1, k = 1.3806 x 10-23 [J/K] is the Boltzmann constant, T is the temperature in Kelvin and R is the resistance value in Ω.

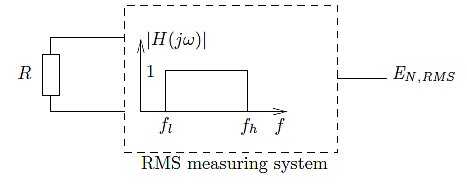
Figure 1 Interpretation of formula EN,RMS = √4kTR·BW

Let’s clarify formula 1 a bit further by looking at Figure 1. EN,RMS is the voltage an idealized RMS-measuring voltmeter would indicate if it had the following characteristics:

• An input impedance equal to infinity
• No internal noise generation
• An amplitude characteristic as shown in Figure 1, with a bandwidth in Hz equal to: BW = fh – fl

You’ll probably argue that’s a lot of conditions; true, but let’s make things a bit more realistic. First of all, the voltage we would measure would be small, so we sure would have to bring in some amplification, say a voltage gain A instead of one. Our meter would then indicate:

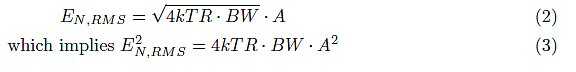
Further, a brick wall characteristic is impossible to realize as it can be proven that such a filter is non-causal. So let’s replace it with a realizable filter characteristic as in Figure 2.

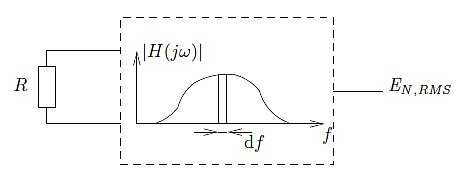
Figure 2 Interpretation of formula EN,RMS for a realizable filter

If we only consider an infinitesimal small bandwidth df, which is the same as applying a brickwall filter with bandwidth df and amplification |H(jω)|, Formula 3 is transformed in:

The quantity

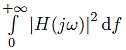
is called the noise equivalent bandwidth (NEB)1. √4kTR is named the noise voltage density, let’s represent it by a stylish ε to avoid confusion with the voltage E itself. So we also could write:

Now, let’s have a closer look at Equation 6. What would happen if we used a filter characteristic with an infinite bandwidth? You might think you could expect an infinite voltage across the terminals of your resistor. This, of course can’t be true in reality. What is wrong here? An explanation finds it roots in quantum phenomena. Formula is not the complete formula, it is only an approximation, indeed the exact formula is: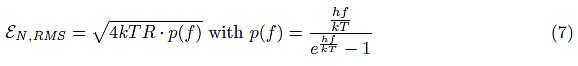

In Formula 7, h = 6.6261 · 10-34 [Js] is the Planck constant. The factor p(f) goes to zero for f going to +∞, this will keep the value of εN,RMS finite. Let’s check this for a system with an infinite bandwidth:

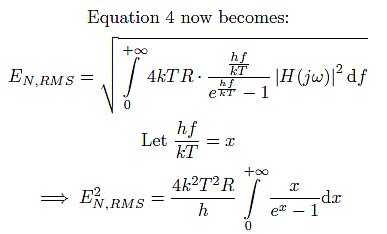
Fortunately, the integral in the previous line, called the Bose integral, has a known neat solution

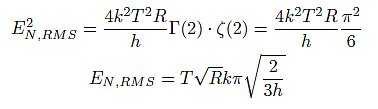
This shows that for a resistance of 1MΩ and a temperature of 300K, the voltage could never become greater than 0.41V. You can also check that the percentual difference in EN,RMS calculated with both formulas for εN,RMS will be at most 1% as long as you stay below 500GHz. Of course you could argue that such frequencies are unrealistic in the world of electronics, but don’t forget these days circuits oscillating at frequencies higher than 1THz have already been built2. produce?

Out of curiosity I checked a few Spice-based simulators –I checked four of them3– to see how well they model noise at these frequencies. Even though they simulate carelessly at extreme frequencies like 10THz, I noticed none of them uses the correct resistor noise model at these frequencies.

Even though this explanation is correct, more practical inclined persons might stay a bit suspicious of explanations stemming from quantum phenomena. Who could blame them as even the late great Richard Feynman said “If you think you understand quantum mechanics then you don’t understand quantum mechanics.” So even though formula 7 explains why you’ll never will get an infinite voltage over your resistor terminals, in practical electronic circuits two other factors will determine the noise contributions of your resistor: a resistor will always have some parasitic capacitance and/or there also will be a bandwidth limitation. The matter of parasitic capacitance is most often dealt with in a standard derivation of the RMS value of the voltage across a resistor in parallel with a capacitor:

again a surprising result when you see it the first time, as the voltage is independent of the value of the resistor. This result can also be explained by resorting to the quantum mechanical world too, see Johnson-Nyquist Noise.

However, there is also an explanation which most electronics people like better or at least convinces them of the result: increasing the parallel resistance will add noise but the bandwidth of the system will decrease such that the overall result remains the same. It’s not difficult to prove this mathematically. However, does this mean that only parasitic capacitance is important? No, as your resistor is normally connected to other parts in the circuit which are bandwidth limited, that also plays a role. The simplest example of such a system is a resistor in parallel with a capacitor followed by a first order system as shown in Figure 3.

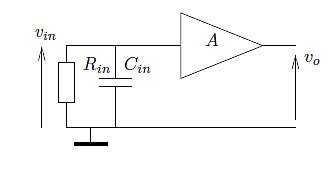
Figure 3 System with input capacitance and a first order amplifier with DC-gain A0 with bandwidth BW

If we call

then we can derive the noise output voltage is given by:

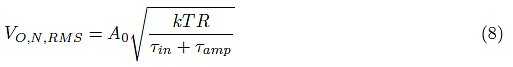
Formula 8 allows you to determine the contribution of the input capacitance (or input time constant) and the bandwidth of the amplifier to the noise voltage at the output. Note that when

the result reduces to:

which comes as no surprise. When

we get as the result:

For practical purposes we can finally deduce the following rule of thumb: when one time constant is at least 10 times smaller than the other, we will make an error smaller than 5 per cent by neglecting the smaller time constant.

Source: EDN article
Hugo Coolens in its EDN article explains in depth resistor noise.

References

1. Some textbooks normalize the NEB by dividing “our NEB” by A2 REF, with AREF the gain at DC or at a reference frequency e.g. the gain in the pass band.
2. Tiny transmitter sets frequency record: Revolutionary terahertz transmitter developed, Technische Universität Darmstadt
3. Spice 2G6, ngspice rev 26, PSpice AD Lite from OrCAD17.2 and LTspice XVII