Switched-Capacitor Circuits Explained

A Switched-capacitor circuit is a fundamental building block of analog IC designs. Jake Hertz explains the basics of its design in an article published by All About Circuits.

One of the most popular approaches for realizing analog signal processing on the IC level is switched-capacitor circuits. Applications for this technology range from filters, AC/DC converters, comparators, telecommunications, and everything in between.

This article will introduce the field of switched-capacitor circuits, starting with a broad overview and then diving into a fundamental circuit block: the switched-cap resistor.

What Is a Switched-Capacitor Circuit? 

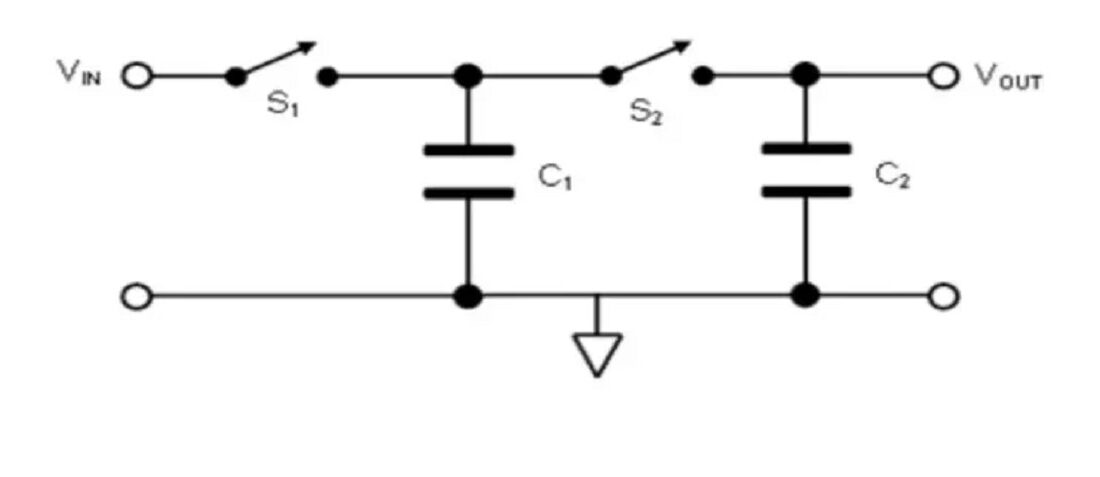
A switched-capacitor circuit is a discrete-time circuit that exploits the charge transfer in and out of a capacitor is controlled by switches. The switching activity is generally controlled by well-defined, non-overlapping clocks such that the charge transfer in and out is well defined and deterministic.

These circuits can be thought of as a type of sample and hold circuit, where values are sampled and passed around through the circuit to achieve the desired functionality.

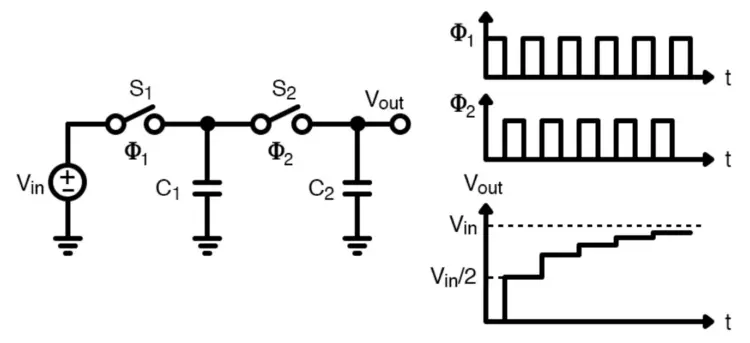
A switched capacitor circuit with non-overlapping clocks. Recreated image by the authors used courtesy of Ma et al.

Switched-capacitor circuits are very popular in applications such as filter designs thanks to their extremely accurate frequency response along with good linearity and dynamic range.

As we’ll see later, the discrete time-frequency responses of switched-cap filters are set entirely by the capacitance ratios and the circuit clock frequency, allowing the response to be set precisely on the order of 0.1%. Continuous-time filters, on the other hand, set their frequency response based on RC time constants, where values can vary by as much as 20% due to process variations.

Switched-capacitor Resistor 

The most fundamental building block of switched-capacitor circuit design is the switched-capacitor resistor. As mentioned, this circuit has two non-overlapping clocks of the same frequency, ø1, and ø2. To analyze this circuit, we’ll look at two stages.

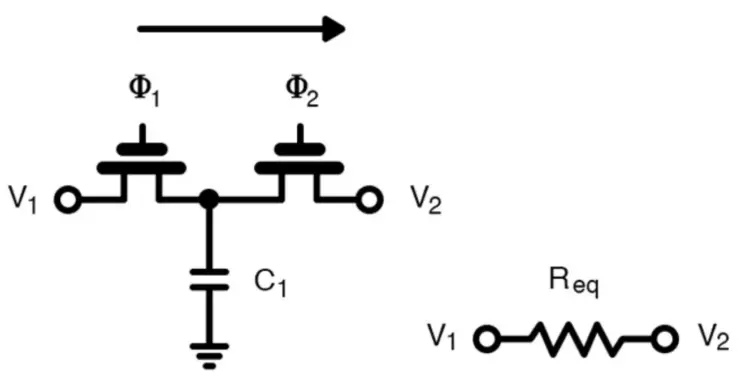
A switched-capacitor resistor. Recreated image by authors used courtesy of Carusone et al.

In the first stage, switch 1 is turned on while switch 2 is turned off. In this setup, the charge flows from node V1 into the capacitor. In the second stage, switch 1 opens while switch 2 is closed. At this point, C1 is connected to node V2 and will either charge or discharge until the final voltage on the capacitor is at V2. The total value of this charge at each stage is given as

Q₁=C₁V₁

Q₂=C₁V₂

If we were to consider the total change in charge, we get the following equations:

ΔQ=C₁(V₁−V₂)=C₁ΔV

Knowing that current is defined as a change of charge with respect to time and that our change in time is nothing more than our clock period, we can get the average value of current across this switched capacitor:

Finally, we can use the above equation to find the equivalent resistance of the circuit:

A quick note: I would be remiss not to mention that the previous analysis assumes that the charge transferred per clock cycle is constant over many cycles, allowing us to approximate average currents and resistances. For situations in which the input signal is changing quickly relative to the sampling frequency, a discrete-time z-domain analysis is required.

Area Savings and Controlled Frequency Response

From these results, we can see the magic of switched-cap circuits: they allow designers to create very tightly controlled resistance that depends only on the clock frequency and capacitor value.

One benefit of this technique is that it helps save space. Achieving large resistances generally requires a sizable amount of silicon area. Both factors can be made significantly smaller with switched-cap circuits.

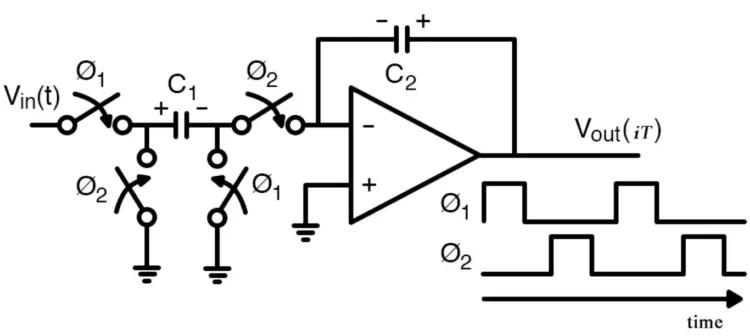
A switched-capacitor integrator with non-overlapping clocks. Recreated image by the author used courtesy of Tenhunen et al.

Another benefit is the fact that mismatch between resistors and capacitors in a continuous-time RC filter is limiting. Matching between similar devices tends to be much better (capacitor to capacitor) as opposed to different devices (capacitor to resistor), making switched-cap filters more precise with their frequency response.

Finally, since our resistance value is set totally by the capacitance value and the frequency, we can dynamically change our filter’s frequency response by changing the clock frequency.

The applications of switched-capacitor circuits are far and wide—and for good reason. Many circuits from filters to ADCs leverage these techniques for their area savings and tightly controlled frequency responses.