Modelling of Supercapacitor Charging Dynamics
- Posted by doEEEt Media Group
- On April 3, 2020
- 0
A new model more accurately predicts the charging time of real supercapacitors by better accounting for the structure of the device’s porous electrodes.
The development of novel electrolytes and electrodes for supercapacitors is hindered by a gap of several orders of magnitude between experimentally measured and theoretically predicted charging timescales. Cheng Lian of Utrecht University in the Netherlands and colleagues have developed a new model, containing many parallel stacked electrodes, that explains the slow charging dynamics of supercapacitors and predicts charging times much closer to real values. The result may help researchers design safer and more effective devices for energy storage.
At low applied potentials, the charging behavior of this model is described well by an equivalent circuit model. Conversely, at high potentials, charging dynamics slow down and evolve on two relaxation time scales: a generalized RC time and a diffusion time, which, interestingly, become similar for porous electrodes. The charging behavior of the stack-electrode model presented here helps to understand the charging dynamics of porous electrodes and qualitatively agrees with experimental time scales measured with porous electrodes.
The porous electrodes used in some supercapacitors are sponge-like materials with nanometer-sized pores. This structure means that they pack a huge surface area into a tiny volume—up to a square kilometer in a cube 10 cm to a side. This property lets a supercapacitor store an enormous charge without requiring a large voltage, making it a safe and space-efficient way to store electrical energy. But the large surface area has a downside: it means they take a long time to fully charge. Previous models represented the electrodes either as single-pore structures that failed to capture an electrode’s vast surface area or as single-plate affairs that ignored their porous structures. These simplifications resulted in the models significantly underestimating charging times.
In their new model, Lian and colleagues approximate the porous structure of an electrode with a series of infinitesimally thin parallel plates that are separated by gaps that are the width of a typical pore. Their model predicts charging times that are off by only a factor of 2 or 3 from experimental measurements of real supercapacitors.
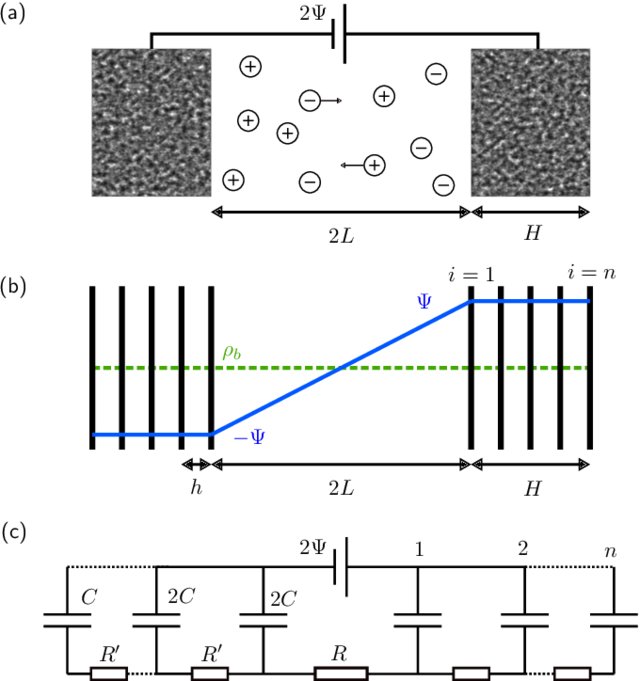
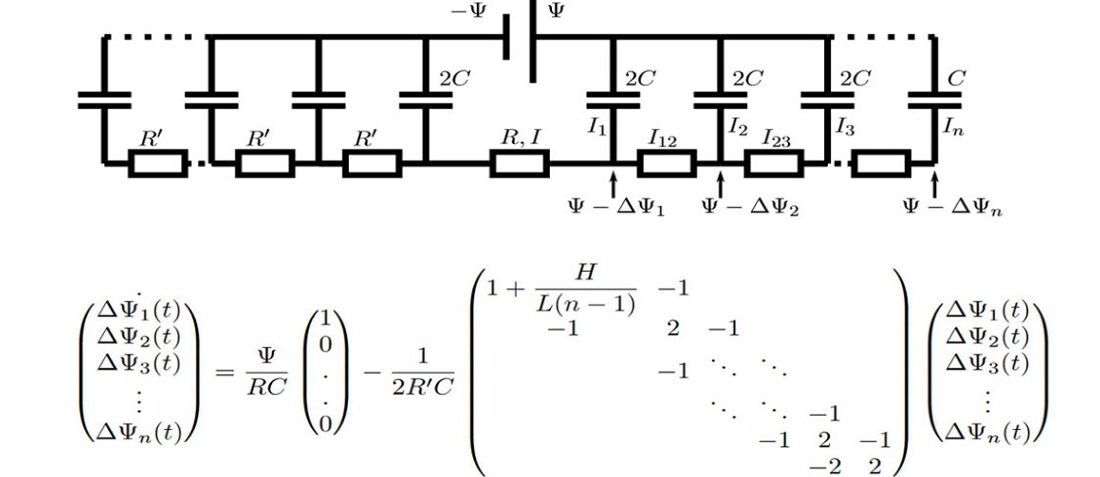
Figure 1. (a) Sketch of a supercapacitor containing a 1:1 electrolyte, two porous electrodes, and a battery providing an electrostatic potential difference 2Ψ. (b) In our stack electrode model, the cathode and anode each contain n planar electrodes at intervals of h. Initial anionic and cationic densities are ρ b throughout the cell. At time t = 0, −Ψ and +Ψ are applied to all electrodes on the left and right-hand sides of the system, respectively. (c) Equivalent circuit model for the stack-electrode model. Source: Utrecht University
In summary, the authors studied the charging dynamics of nanoporous electrodes with a simple electrode model. A small applied potentials, numerical simulations of the PNP equations are reproduced accurately by an equivalent circuit model.
This circuit model is akin to TL models used often to fit experimental supercapacitor data. Notably, however, the resistances, capacitance, and number of branches in the circuit model are not fit parameters but physically determined by the evaluated microscopic model.
This one-to-one relation allows to interpret the long relaxation time of supercapacitors as being due to a large number of pores in nanoporous electrodes: The stack-electrode model relaxes with the time scale τn∼(2 + 0.75H/L)nτRC.
At higher potentials, the surface charge still relaxes at early times with τn. Higher potentials also lead to slow salt adsorption in the EDLs and concomitant depletion of the reservoir on the time scale τad∼(L+H)2/D. As salt and charge transport are coupled, the long time scale τ ad also governs the late-time surface charge relaxation, all the more so the higher the applied potential.
The two time scales τn and τad differ orders of magnitude for small n but become similar when electrodes have many pores, as is the case for supercapacitors. Inserting parameters relating to a re-ent experimental study, the simple model predicts the two observed relaxation times roughly within 1 order of magnitude.
The model thus successfully bridged the 5-orders-of-magnitude gap between theoretically predicted and experimentally measured timescales, and could serve as a basis for extensions that break the planar symmetry. However, more work is needed to fully understand the charging dynamics of porous electrodes, which should include effects due to finite ion sizes, more realistic modeling of pore morphology, Faradaic reactions, position-dependent diffusion coefficients, etc.
- Researchers Demonstrated Novel BTO Based Capacitor Heterostructures with 19x Higher Energy Density - July 24, 2024
- Passive Components Electrodes and Terminations - July 24, 2024
- BJT Filters and Capacitance Multipliers - July 22, 2024

0 comments on Modelling of Supercapacitor Charging Dynamics