The time constant of capacitors is the time needed to discharge a loaded capacitor through the insulation resistance (IR) to 1/e (~37%) of the initial voltage. This constant, denominated t(tau), is the product of IR and C (capacitance), usually abbreviated RC. Supercapacitors don’t have any dielectric even if the actual leakage current represents a kind of “internal DC resistance.” What is of importance to supercapacitors is their ability to absorb and release electric charges. This depends on their ESR. The more conductive the electrolyte and the better construction that facilitates the current flow, the lower the ESR and, consequently, the faster the charge and discharge time.
Some supercapacitors have many time constants, while especially power-burst designs are characterized by tiny ones, ranging from milliseconds to minutes.
Supercapacitors’ Energy Density (Wh/kg) and Power Density (W/kg)
Compared to conventional electrolytic capacitors, Electrochemical capacitors have approximately 10-100 times higher energy density (also called specific energy) expressed in Wh/kg. If we compare it with traditional electrostatic capacitors, the particular energy is approximately 100 times higher. Despite supercapacitors being subjected to fast developments, batteries may typically have 10 to 100 times as much energy density (as battery development is also significantly moving forward).
Comparisons on power density show another picture. Electrochemical capacitors having considerable ESR values and time constants of 1 to 100 seconds equal batteries concerning power density. In recent years, marketed power supercapacitors have been able to deliver ten times the power of conventional batteries or, with the latest graphene electrode design, can get very close to electrolytic capacitors. Their time constants range from below 0.1 seconds to 30 seconds.
Applications
As mentioned in the introduction, supercapacitors seem very reliable, claiming a service life exceeding ten years. Together with capabilities of charge/discharge cycles ranging to millions, they offer maintenance-free products of high interest, especially when combined with rechargeable batteries. They have a high power density, and their capacitance ranges from several farads to several thousand farads, making them perfect for high power-burst applications. Nevertheless, watch for low-end “no-name” supercapacitors, as there are also “cheap” technologies on the market with significantly worse capacitance drop versus cycles/lifetime or operation at higher temperatures.
High power-burst applications can be divided into two categories. The first one is small-cell designs. They belong mainly to applications like digital cameras, wireless PCs, and the like, where they are used to load-level pulses from energy sources such as batteries and fuel cells.
The second category is large-cell types. For example, they will be found in automotive applications and as UPS (uninterrupted power supplies) in industrial applications. Whether small-cell or large-cell supercapacitors are utilized in power-burst applications, they will relieve the battery of pulsed power functions. That means the possibility of utilizing smaller power batteries is high.
In electrical vehicles (EV) and hybrid electric vehicles (HEV), a combination of batteries and supercapacitors provides high immediate power and a longer energy supply. The supercapacitor is also a popular solution for start-stop systems integrated into vehicle energy recuperation energy management systems to lower combustion engine vehicles (CE) and HEV emissions and consumption. As already mentioned, these supercapacitors can deliver more than ten times more power than batteries. Especially at lower temperatures, where the power supply from batteries might be insufficient,, supercapacitors can be the solution. Some of them can operate successfully down to –40°C. Batteries have minimal power in the cold, and the power supply for starting may be pretty insufficient. On the other hand, they can trickle-charge the supercapacitor that, in turn, has the power necessary for creating.
Many of these supercapacitors can be discharged down to 0 V. On the other hand, one major limitation of supercapacitors blocking the complete replacement of batteries in combustion engine vehicles is their higher self-discharge/DCL and its significant increase at higher temperatures – see further below and illustration in Figure 21.
Charge and Leakage currents
In aqueous electrolyte constructions, as well as in some organic electrolyte types, we could, concerning time, distinguish three different types of current components:
- a charging current, Ich,
- an absorption current, Labs,
- a leakage current, DCL.
The charge current charges the different capacitor elements. A large part of this “operating charge” can occur within fractions of a second but the exchange increases if we extend the time to minutes or even more. Even if ESR limits the surge current at rapid charges/ discharges, a current limiting resistance of the same magnitude as the ESR is recommended.
As was seen in the previous section, there is an extensive distribution of time constants for the different capacitor elements. The most inert ones never charge within a reasonable time. Once set, they won’t participate in discharges under a specific practice time. They have been absorbed. The so-called absorption current characterizes the absorption process during charging.
After a very long charging time, we reach a limit for all charging currents. There is a current left, the actual leakage current. In reality, it is independent of time since it always exists. Figures 12. and 13. show examples of the three current components and their time dependence.
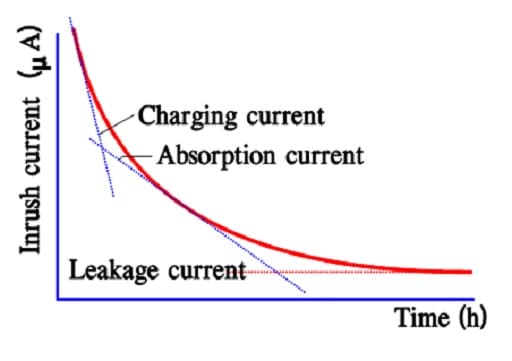
Figure 12. The three components of the inrush current in a double-layer supercapacitor.
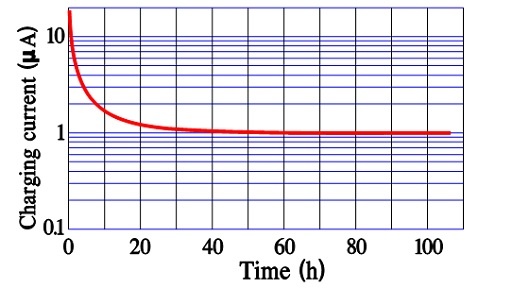
Figure 13. An example of Inrush current versus time in an older double-layer supercapacitor.
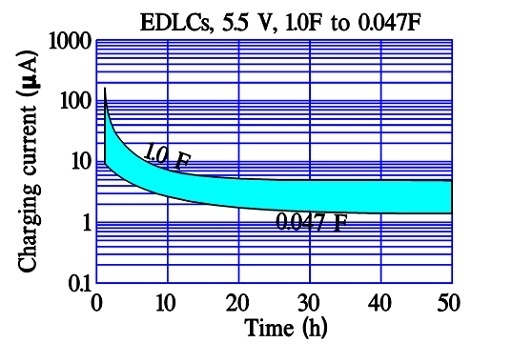
Figure 14. Examples of inrush currents versus time in double-layer supercapacitors.
In modern power supercapacitors, the charge/discharge times are so small that no significant difference exists between the first two current components discussed above.
Measurements
Leakage current
The leakage current, DCL, is sometimes called bias current and is specified after 10, 30, or 60 minutes of applied rated voltage, as seen in Figures 12. and 13. these times are too short for an accurate DCL determination. For reciprocal comparisons, however, they serve their purposes.
Remarkably, some manufacturers of power supercapacitors (where the charge/discharge time is specified from 0.3 to 30 seconds) specify DCL measurements after 12 or 72 hours of applied rated voltage.
Capacitance
Despite decreasing ESR values in modern designs, AC capacitance measurements are considered inaccurate. Instead, a discharge with constant current is resorted to (Figure 15.).
The capacitance determination is based on the fundamental formula Q = C x V. But, at constant current, Q = I x t.
According to the figure, C x (V1-V2) = I x (t2-t1).
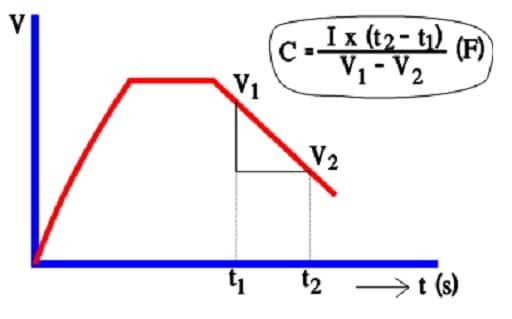
Figure 15. Principle of capacitance determination of a double layer supercapacitor.
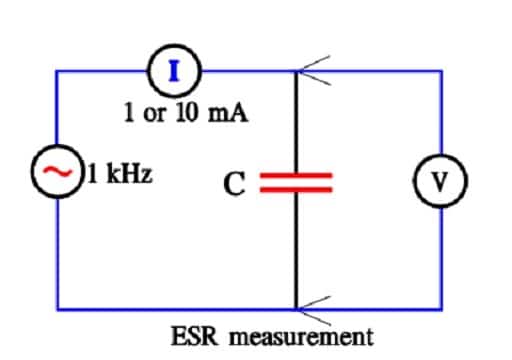
Figure 16. Determination of supercapacitor ESR.
ESR
ESR is measured at 1 kHz and a constant current of 1 or 10 mA.
Life calculations
Supercapacitor manufacturers mainly specify estimated life versus voltage and temperature. Nevertheless, it can be specific to the supercapacitor technology, so it is recommended to check the manufacturer datasheets.
Roughly the life will be reduced by more than two times (more accurately 2.23 times) for every 10 degrees C increase. If we use the formula [1], it should be written as:
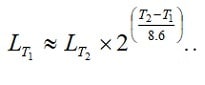
[1]
Life dependence of working voltage can be expressed with the formula [2]. Because we deal with electrolytes the exponent is significantly higher than that of electrostatics, i. e., n » 17, which gives us the following equation:
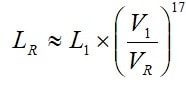
[2]
According to the manufacturer’s graphs (and the formula above), there will be an approximate halving of life for every 4.4 % voltage increase above VR and a corresponding life increase for derating with 4.4 %.
Environmental operation risks
Avoid the use of non-hermetic types at:
- environments with a high RH
- corrosive gases
- cleaning agents with Freon TMC or Trichloro-ethylene.
Characteristics
Discharging
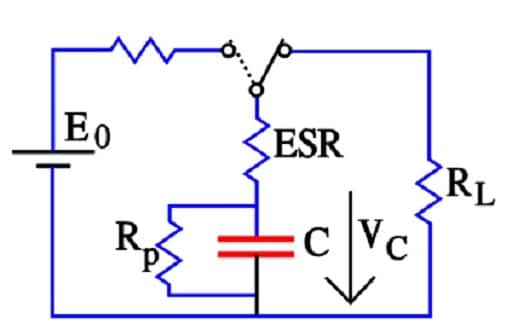
Figure 17. Discharge of a supercapacitor with an inductive load RL
At a discharge of the capacitor, the voltage follows the equation
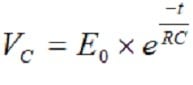
[3]
, where:
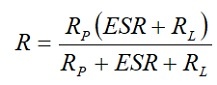
[4]
But at 1 to 100 mA load RL,>> ESR and Rp >> RL. Then R ≈ RL and the discharge time t = – CRL ln(VC/E0). Semiconductor memories, on the other hand, will draw less than 10 *A. In these cases, RL >> ESR and
R ≈ RpRL/(Rp+RL).
The following diagram in Figure 18. is taken from either of the established manufacturers and may differ between the manufacturers.
Discharge current versus backup time
Manufacturers of supercapacitors used for backup purposes specify voltage versus backup time/holding time for different discharge currents. The time is related to discharge from rated voltage down to 2 V (where its backup function ends).
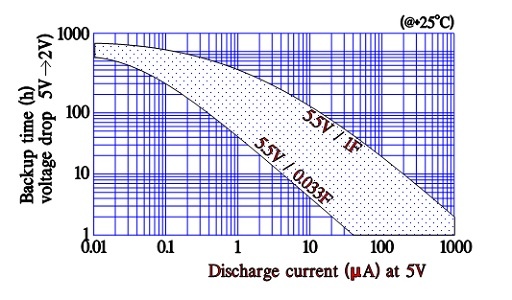
Figure 18. Supercapacitor backup time versus discharge current and capacitance.
Discharge conditions
The following figure shows a diagram of constant-current discharge curves for an EDLC supercapacitor with an ESR of a maximum of 120 ohms at 1 kHz. Note the sudden voltage drop of 0.5 V in the one mA curve. It is related to the internal DC resistance. At 0.1 mA, it is not visible.
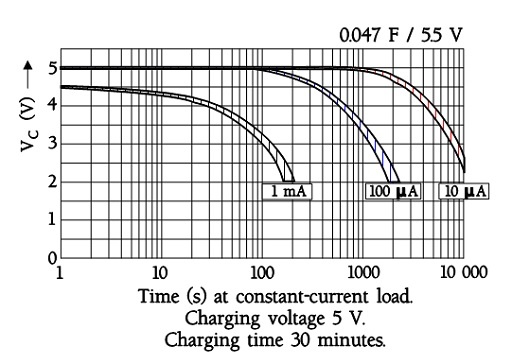
Figure 19. Example of discharge diagrams for a button cell EDLC supercapacitors.
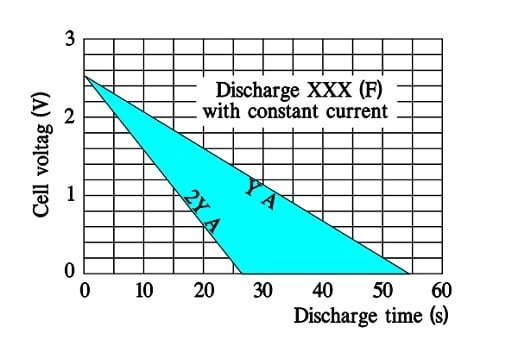
Figure 20. A typical discharge diagram for a large supercapacitor.
Discharge curves for ultracapacitors with small ESRs exhibit straight discharge curves. Fictitious curves for a large supercapacitor capable of a discharge to 0 V may have the following appearance where the discharge currents are called Y and 2Y (A).
Note that doubling the discharge current means halving the discharge time.
Self-Discharge
The internal leakage of electric charges will gradually decrease the initially applied voltage. The following two figures illustrate the phenomenon.
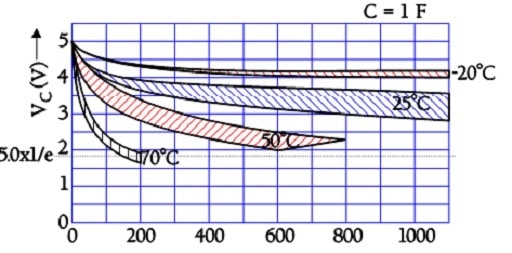
Figure 21. Examples of a supercapacitor temperature-dependent voltage drop at open circuit conditions and an internal leakage through the insulation resistance (self-discharge).
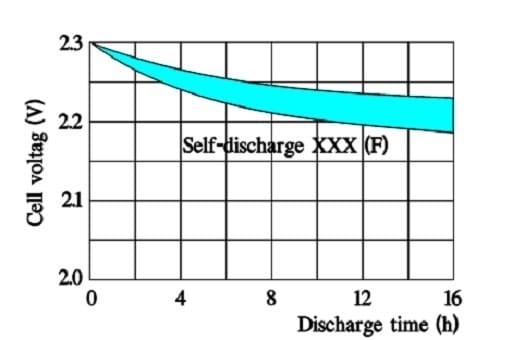
Figure 22. Typical appearance of the self-discharge curve for a larger supercapacitor with VR = 2.3 V.
The above figure shows that the time constant – i.e., the time it takes for the voltage to drop to 1/e of the initial voltage – is considerable, even at +70 °C. Larger supercapacitors characterized by lower ESR values may have the following self-discharge curve. Always consult the manufacturer for accurate specifications.
Temperature dependence
The typical capacitance dependence of temperature may look like the following curves in Figure 23.
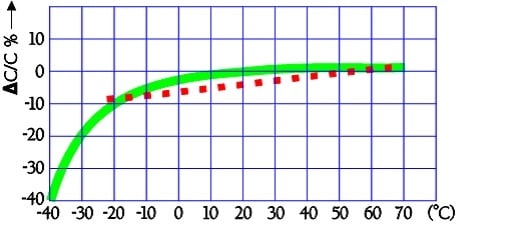
Figure 23. Typical examples of capacitance versus temperature. The bald-line curve represents a high-ESR carbon double-layer capacitor, and the dotted line is a solid electrolyte EDLC.
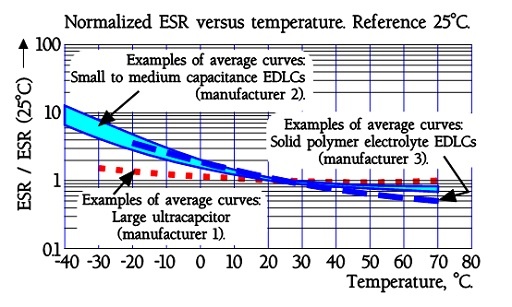
Figure 24. Normalized EDLC supercapacitor ESR versus temperature.
The quotient ESR-25°C / ESR+20°C will be ≤ 5. Larger modules are specified ESR-25°C / ESR+20°C ≤ 10.
The following diagram shows curves for the temperature dependence of the leakage current in older aqueous electrolyte capacitors. Because the actual double-layer construction is also valid in newer EDLCs, we have reason to believe that the temperature dependence is still present even if the magnitude may differ.
The leakage current examples in Figure 25. are based on readings after 60 minutes of electrification with 5.5 V dc. Charging for 10 or 30 minutes will, of course, give other values.
The quotient DCL70°C /DCL 20°C will be ≤ 4.
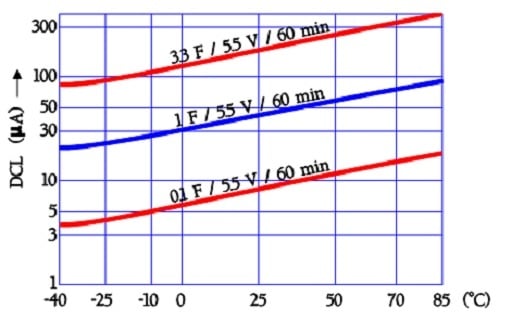
Figure 25. Examples of EDLC supercapacitor leakage current versus temperature.
Source: Epci Blog

