Capacitor Losses (ESR, IMP, DF, Q), Series or Parallel Eq. Circuit?
- Posted by doEEEt Media Group
- On February 22, 2023
- 0
This article explains capacitor losses (ESR, Impedance IMP, Dissipation Factor DF/ tanδ, Quality FactorQ) as the other basic key parameter of capacitors apart from capacitance, insulation resistance, and DCL leakage current.
There are two types of losses:
- Resistive real losses – these are real losses caused by the resistance of leads, electrodes, connections, etc. During current flow, these losses are dissipated by Joule heat. Usually (unless it is intended by design) the effort is to minimize these losses for maximum efficiency and high power load ratings.
- Reactance imagine losses – these are losses caused by capacitive reactance and inductive reactance “stored” in the component that can be reverted back
A capacitor creates in AC circuits a resistance, the capacitive reactance. There is also certain inductance in the capacitor. In AC circuits, it produces an inductive reactance that tries to neutralize the capacitive one. Finally, the capacitor has resistive losses. Together these three elements produce the impedance, Z.
If we apply an AC voltage over a capacitor, its losses release heat. They can be regarded as a resistive part of the impedance, i.e., as resistive elements distributed in different parts of the component, e.g. in accordance with the equivalent circuit in Figure 1.
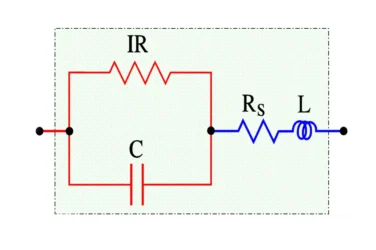
Figure 1. Circuit diagram of a capacitor
- C = Capacitance
- IR = Insulation Resistance (IR>>Rs)
- Rs = Series losses
- L = Inductance in lead-in wires
Rs consists of resistance in lead-in wires, contact surfaces, and metalized electrodes, where such elements occur, and dielectric losses. If we apply a DC voltage over the capacitor, the generator ”feels” a purely resistive loss dominated by the IR. But because of the high value of the IR, the heat release will be negligible. If we change over to an AC voltage and let the frequency rise, the current will increase proportionally and eventually release considerable heat in the Rs. Suppose we transform the IR to a small series resistance and join it with the Rs. In that case, we get a total series resistance called ESR (Equivalent Series Resistance, sometimes called Effective Series Resistance). The series impedance, Zs, in Figure 1. can be written:
As a root mean square value, we obtain the formula:
(Ω)……………………… [1]
The capacitive reactance, 1/ωC, in the formula above decreases with frequency to that level where the inductive reactance, L, takes over. It happens at the resonance frequency fo of the capacitor where 1/ωC = L. Above the resonance frequency, the capacitor is inductive. Exactly at the resonance frequency remains the impedance Z only the resistive ESR (Figure 2.). By determining the losses at the resonance frequency, we gain accuracy. But there is a condition for this accuracy. We need to know the frequency dependence of the ESR, which is very much conditioned by the dielectric material. It isn’t very important in certain materials, but in others considerable.
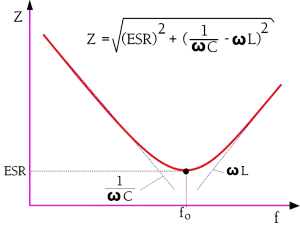
Figure 2. The impedance diagram of a capacitor
The expression for capacitance in the formula for Zs above can be simplified to a series capacitance Cs. If C means the nominal capacitance then we obtain Cs as
………………………… [2]
and
………………………… [3]
The equivalent circuit diagram then looks like the one in Figure 3.
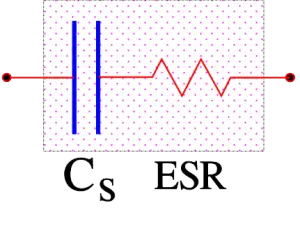
Figure 3. The equivalent series circuit diagram of a capacitor. Valid at higher frequencies
Impedance around the resonance frequency
Figure 2. shows an example of the impedance diagram around the resonance frequency. We shall evolve the reasoning further.
Because of the approximations used during the derivation of the formula [2] it applies only far below the resonance frequency, f0. There, however, it may cause discernible deviations from the true value. Already at 0.2 x f0 Cs will be approximately 4% greater than the nominal value C.
Often the expression for Cs is used when the frequency dependence of capacitance is shown in diagrams. This means that the capacitance quite contrary to physical and electrical laws, starts rising at higher frequencies. The explanation accordingly is to be sought for errors in the measurement method.
Except for electrolytes and other high-loss capacitors, the impedance curve usually has the appearance of the one shown in Figure 4.
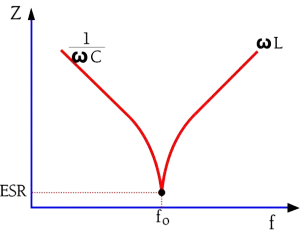
Figure 4. The appearance of the impedance vs. frequency curve around the resonance frequency in low-loss capacitors
The sharp tip at the resonance frequency is typical for capacitors with comparatively small losses. In this frequency range, the impedance contribution from the ESR is smaller than those of the capacitive and inductive reactances. When the decreasing capacitive reactance reaches the same magnitudes as those of the rising inductive reactance, the latter will have an increasing influence. It reduces the capacitive reactance and eventually eliminates it. The curve bends down in a sharp tip. The ESR determines the bottom of the bend.
In capacitors with relatively high losses, for example, electrolytes, the impedance curves reach and are influenced by these losses long before we get to the resonance frequency. A frequency-dependent decrease in capacitance may also play a certain role in the frequency range. The impedance curve will deviate from the initial reactance curve and level out in a pliable bend on the ESR contribution, high above the point of intersection between the capacitive and inductive branches. The phenomenon is illustrated in Figure 5.
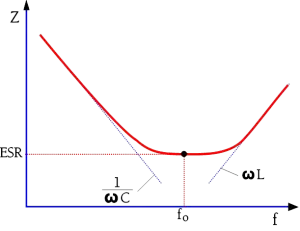
Figure 5. The appearance of the impedance vs. frequency curve around the resonance frequency of high-loss capacitors
Loss Dependent Derating
The heat release from AC applications limits the temperature range of paper capacitors, where the loss raises the internal temperature appreciably. While DC applications allow +85 or +100°C, AC applications already at 50 Hz may require limitations to a maximum of +70°C.
Higher frequencies require further derating because of the current, which grows correspondingly. The R.M.S. value of the AC voltage furthermore is derated according to the permitted DC value not only concerning the peak value and the temperature rise but also because of the additional strain that every repolarization exerts on the dielectric. The higher the rated voltage, the higher the degree of derating.
Example: AC/DC = 40/63, 63/100, 125/250, 220/400, 300/630, 500/1000, 660/1600. But please, always check what the relevant data sheets specify.
The losses in Figure 6. are concentrated in the ESR, which becomes significant when we leave the low-frequency range. For HF chips and high-loss components for example, electrolytes often the ESR is stated in the data sheets. If the ESR information is missing, you always find, for all component types, a specified dissipation factor (DF), the tanδ (Figure 6).
Hence at higher frequencies, the series circuit according to Figure 3 applies. There is
……………….. [4]
Tanδ usually is expressed in %.
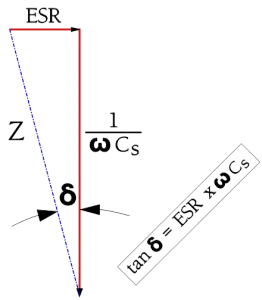
Figure 6. Definition of Tanδ in a series circuit
If the frequency declines to zero, the circuit becomes resistive, without any capacitance, and the losses are limited to the IR. Also, at very low frequencies, the IR is predominant, but here it should be completed with dawning AC-dependent losses to an equivalent loss resistance Rp. The diagram in Figure 2. can now be simplified to a parallel circuit with the capacitance Cp (Figure 7.).
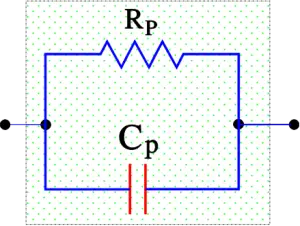
Figure 7. The equivalent parallel circuit of a capacitor. Applies at low frequencies
If we describe the impedance in a parallel circuit according to Figure 7. it’s easy to show that its dissipation factor – which applies at low frequencies – can be written as
……………………………[5]
The difference between Cs and Cp usually is negligible depending on the impedance value – see note below. We shall return to the connections in some formulas. If we equate the formula [2] with [3], we obtain
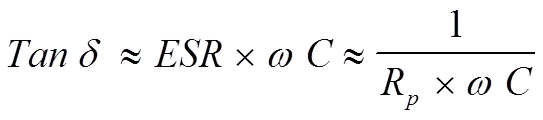
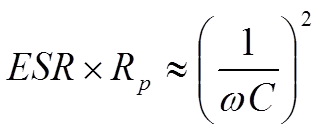……………………[6]Let us terminate the discussion about the capacitor losses by distinguishing the different types of losses as in the following Figure 8.
Q value Dielectric Quality Factor
Sometimes we encounter the Q or Q value, especially in high-frequency applications. Instead of describing the capacitor losses as DF (Tanδ) we rather specify its freedom from losses, its figure of merit, the Q value. It is defined as
…………………….[7]
Typical Q values for ceramic Class 1 dielectric range from 200 to 2000 at 100 MHz and will vary strongly with frequency.
We shall use the Q value to describe the connection between the quantities in the series and parallel circuits in Figures C1-18 and -20. By depicting the expressions for the impedance and Q values of these circuits and equating the real and imaginary parts of the impedance, we can show that
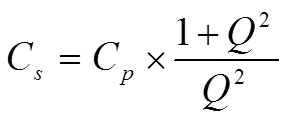………………………………[8]
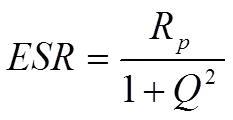…………………………………….[10]
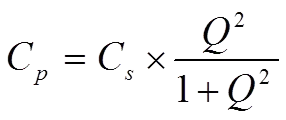…………………………[9]
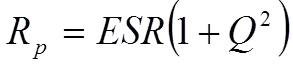……………………………[11]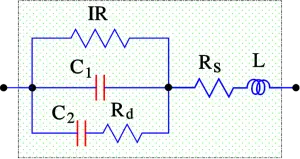
Figure 8. Equivalent diagram with dielectric losses particularly marked
- Rd = dielectric losses
- Rs = losses in leading-in wires, joints and electrode metallizations
- ESR = Rs + Rd
- C = C1 + C2.
Cs, Rs or Cp, Rp What to use for impedance measure bridge setup?
An impedance analyzer can measure the capacitance both in parallel or in series. The best-fit circuit model will depend on the capacitance value of the capacitor.
When C is small and the impedance is high, the parallel impedance between C and Rp will become significantly higher than Rs. Thus the meter setting for measuring capacitance should be Cp. When C is large, and impedance is small, parallel impedance for C and Rp is not as significant. Therefore, Cs should be used for the meter set to measure capacitance.
A good rule of thumb for selecting the impedance setting is to use Cp for capacitor impedance values greater than 10kΩ and Cs for less than 10Ω.
ESR or DF?
Another practical outcome is considering what parameter better describes losses in a capacitor – ESR or DF? From the pure physics point of view, it does not matter, as together with a second parameter (capacitance or impedance), both parameters describe the same stage of the capacitor. While ESR is information about real losses only, DF combines information about real losses and reactive losses (but we need the second parameter anyway to describe the exact capacitor stage).
The same is true about ESR/DF frequency dependence. It does not matter if I use ESR or DF characterization for description at low or high frequencies from basic physics. However, the industry convention is to use DF for low-frequency (120Hz or 1kHz) characterization, where dielectric losses dominate, and ESR for higher-frequency (100kHz) behavior, where resistive connection losses are the main part of the losses. You can find DF and ESR values in manufacturer datasheets concerning those frequencies.
Case study: you can hear people from the industry saying: “that capacitor has a high DF” that means that the capacitor has a high loss in the lower frequency zone (120/1kHz) that could indicate some issue with dielectric material (impurities, delamination …). and of course, ESR at 120Hz/1kHz will also be high. The same is about ESR – when someone says: “ESR of the capacitor is a problem,” he/she usually means a reference to the standard measurement frequency 100kHz indicating problems with resistive losses (inter-connection issues, bad welds, etc.) … and of course, DF at 100kHz would also be high.
Just in the range where the reaction time of the dipoles and the frequency period coincide, a kind of resonance occurs which causes the dipole types to react with a loss peak (Figure 9).
Observe that Figure 9. deals with dipole losses, nothing else. Other dielectric materials have no molecular dipoles. They are called non-polar, while the others are called polar. This has nothing to do with the polarity dependence of electrolytes.
The sum of losses in a polar and a non-polar capacitor may look like the ones in Figure 10.
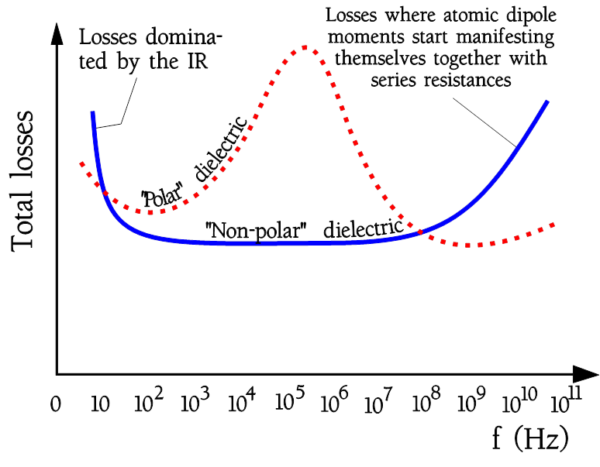
Figure 10. Total losses versus frequency in a polar and non-polar dielectric material
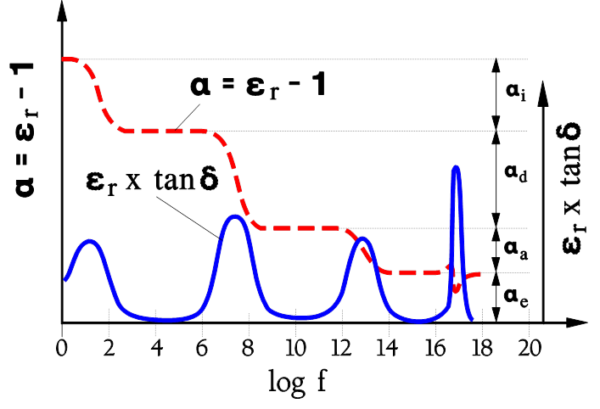
Figure 9. Dipole losses versus frequency
Figure 9. illustrates the behavior of different dielectric dipoles when they are affected by an alternating field. They will oscillate at the same frequency as the fields if allowed by their reaction time. Every rotary motion requires energy, and the executed work produces heat. The most inert dipoles will react to very low frequencies and contribute to the losses. But as the frequency increases, the different types of dipoles will not be able to respond quickly enough, one after another, as shown in the figure.
We shall remember that dielectric losses (material permittivity) may be frequency dependent. As per the basic capacitance calculation, it is the only parameter responsible for capacitor frequency dependence in the ideal capacitor (considering the surface area of electrodes and thickness of dielectric stable). The real capacitor may have an additional RLC ladder structure that limits its resonance and maximum operating frequency.
A team of experts that brings you the latest and most important news about the EEE Part and Space market.
- Managing EEE components for LEO and lower cost space missions - December 17, 2024
- Filtering Characteristics of Parallel-Connected Fixed Capacitors in LCC-HVDC - November 21, 2024
- ALTER SPACE TEST CENTER: testing approaches for New Space - September 30, 2024
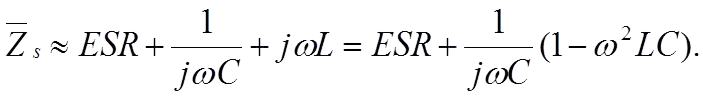
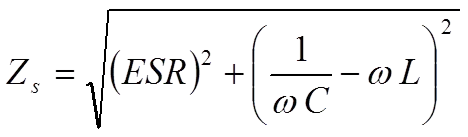
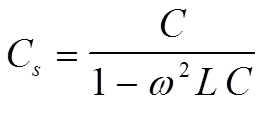
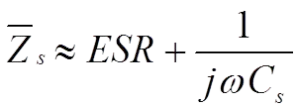
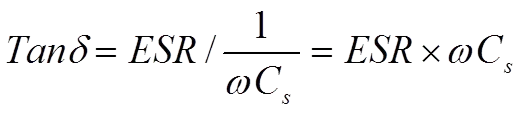
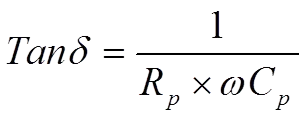
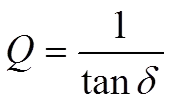
0 comments on Capacitor Losses (ESR, IMP, DF, Q), Series or Parallel Eq. Circuit?