The ideal capacitor Cs is influenced by the lead inductance Ls (of the order of several nH) and the track resistance Rs (typ. of the order of 20 mΩ … 100 mΩ, for cold electrolyte capacitors up to 1 Ω). At low frequencies, the capacitive component predominates, and at the self-resonant frequency, the track resistance is measurable. Above the series resonance, the inductive component predominates, which may, to some extent, be influenced by having short connecting lengths. The phase curve changes from ≈ –90° to ≈ +90° in the region of resonance. The phase point 0°, therefore, precisely defines the point of resonant frequency, often much more precisely than is possible by means of amplitude measurement. The phase curve also serves the computer-aided determination of the equivalent circuit (1st approximation).
Inductance → parallel resonance
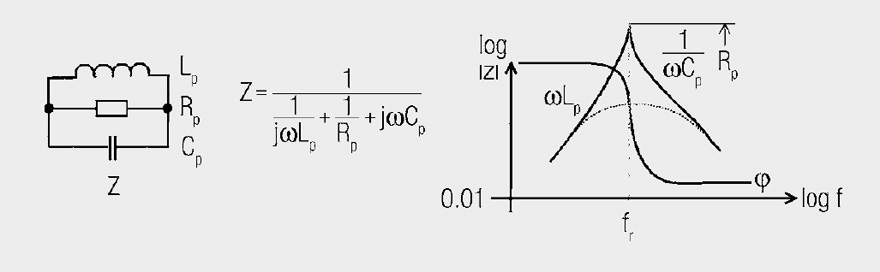
Fig. 2: Parallel circuit and impedance against frequency
The ideal inductance Lp is influenced by the unavoidable winding capacitance Cp and the assimilated Rplosses (core material, winding losses). An infinitely large parallel resistance Rp is desirable for inductors, for EMC ferrites, on the other hand, a very low and broadband resistance Rp is the desired parameter. The inductance Lp plays a lesser role and is the key to transforming the resistive loss into the line.
This means that in the model, in the place of the EMC ferrite, the line is cut open and the equivalent circuit is interposed. A component is only exactly described by all three parameters L, C and R. A single parameter is insufficient, although other properties may be predicted for known configurations.
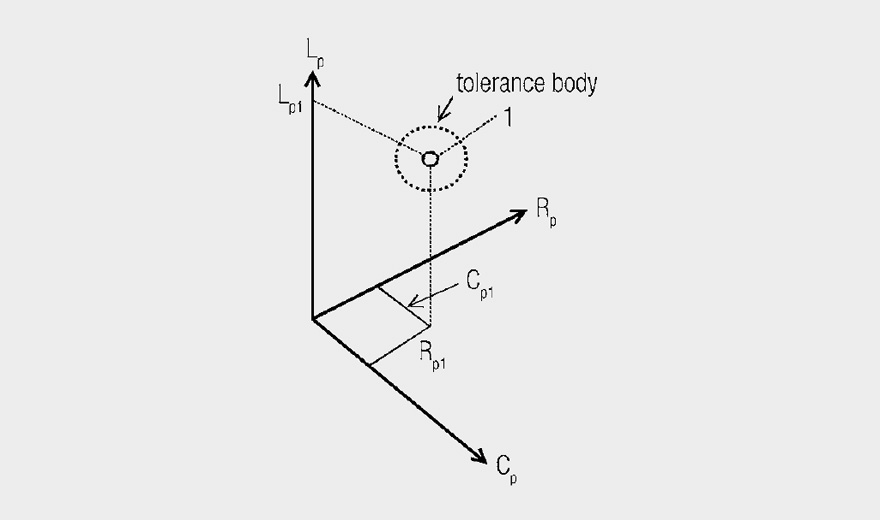
Imagine a three-dimensional coordinate system with the axes Rp, Lp, Cp; the component is a point in this space and its tolerance field is a cuboid body. Various components are located in this tolerance space as different points.
This mathematical treatment of series and parallel resonance may be summarized as follows:
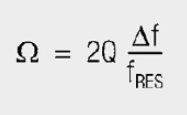
Unified (normalized) resonance curves for series and parallel resonant circuits as a function of the normalized imbalance Ω in all the values of L, C and R are included. Standardized detuning unifies the parameters of quality factor and resonant frequency fRES. This makes it easier to describe the behavior of resonant systems in their frequency range.
(Δf … frequency deviation from the resonant frequency)
Series resonant circuits:
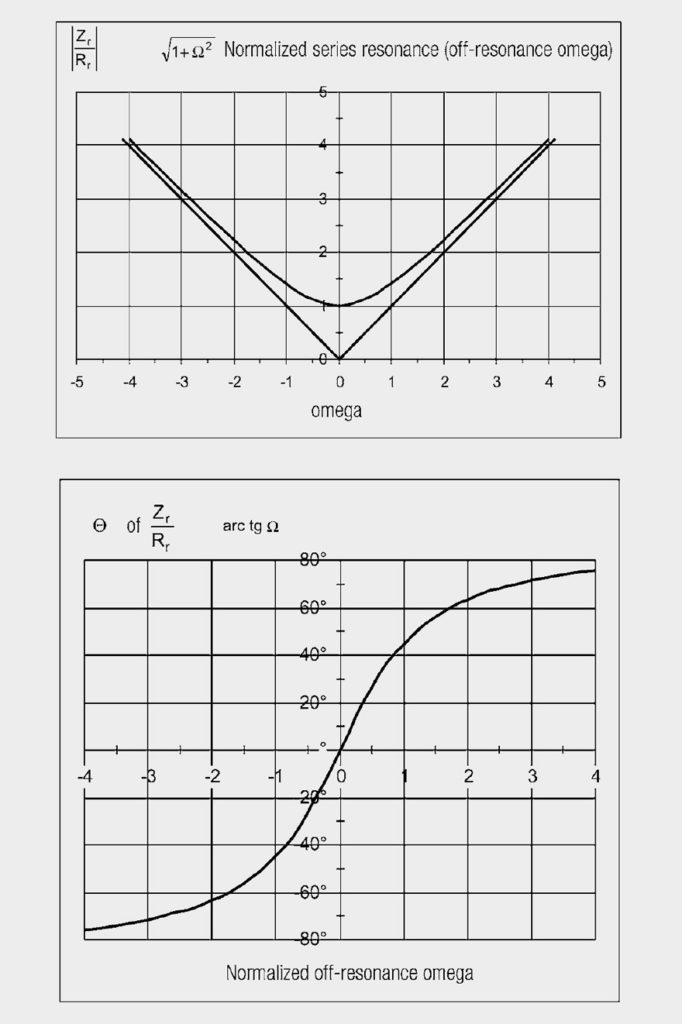
Fig. 4: 1 + jΩ (magnitude and phase) as a function of Ω
Parallel resonant circuits:
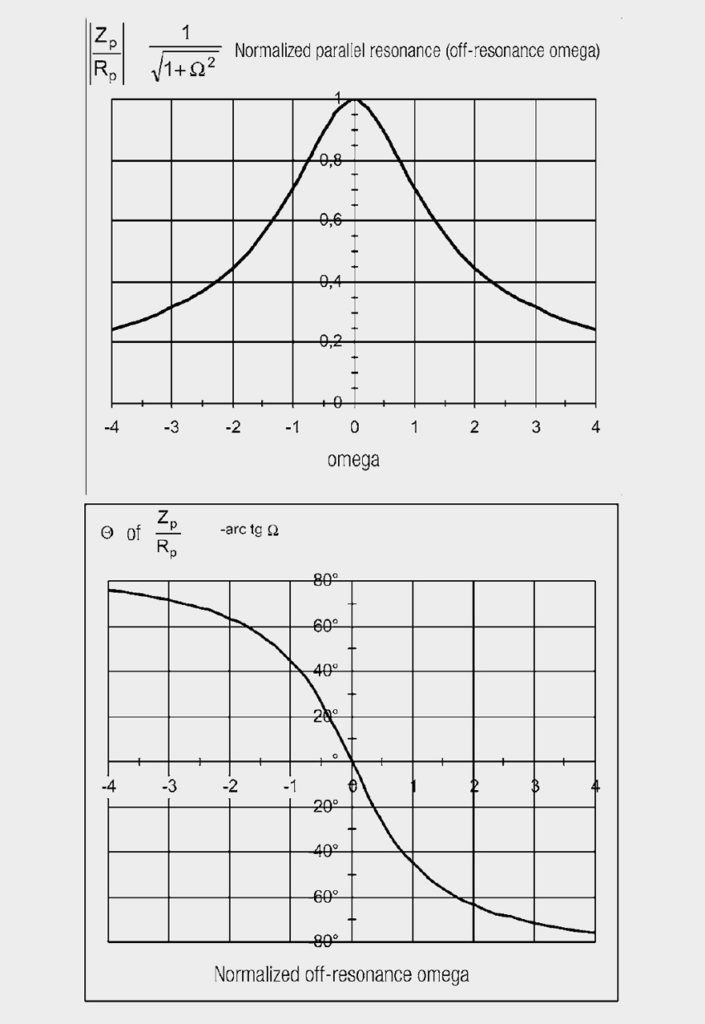
Fig. 5: 1 / 1 + jΩ (magnitude and phase) as a function of Ω
Series resonance
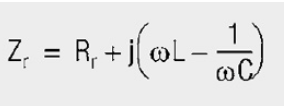
Resonant condition:
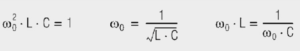
for parallel resonance:
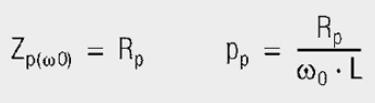
for series resonance:
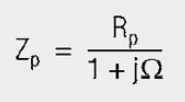
Parallel resonance
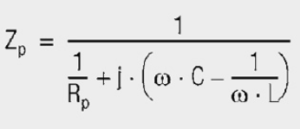
for series resonance:
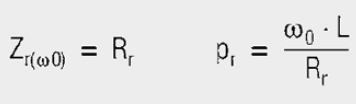
Normalized off-resonance:
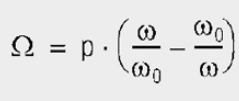
for parallel resonance:
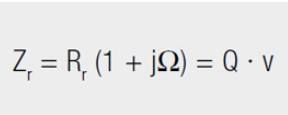
The detuning v denotes how far the resonant circuit is detuned compared with the imposed oscillation. In short: Measure of the deviation of the (circuit) frequency from the resonant (circuit) frequency.
The normalized curves are plotted in Figures 4 and 5 for R = 1 (top magnitude, bottom phase).
Selecting the suitable operands (normalization), it is possible to illustrate all characteristics as two standard curves. They serve to provide a basic understanding, whereas, in applications, the measured resonance curves are evaluated or in computer simulations, the numerical values of L, R, and C.
Derivation of simple equivalent circuits
In the following examples, measurement curves derived with the HP 4195 are analyzed. It is however in principle irrelevant with which measuring device or configuration the curves are derived.
The analysis is based on fundamental theoretical modeling concepts.
Figure 6 shows the impedance of a small air coil of 6 mm diameter and 6 winding turns. A simple estimate of inductance from the values at 10 MHz and 100 MHz gave an L of 63.7 nH. As the phase Θ is between 85°–90°, one may assume a pure inductance and obtain from |Z| = 4 Ω at 10 MHz and |Z| = 40 Ω at 100 MHz.
The analyzer measures L = 58 nH as a result of its more accurately stored values than those displayed. Two curves are just distinguishable in Figure 6, a thick measurement curve and one, which the analyzer plotted as the result of its equivalent circuit measurement. It actually includes an equivalent circuit calculator. It calculates the equivalent circuit plotted in Figure 6 and writes the calculated values of |Z| and Θ alongside the measurement curve. Without a computer, one would have to be content with just a rough calculation.
Multi-dimensional measures are required in EMC matters; precision is not of paramount importance.
Figure 7 shows the impedance curve of a ceramic disc capacitor of 10 nF capacitance rating with approx. 5 mm long connecting legs. By reading the measurement curves and calculation, C = 11.37 nF and L = 9.55 nH could be found. From the |Z| curve at Θ = –90°, the capacitance
And at Θ = + 90° the inductive component
|Z|200 kHz = 70 Ω, |Z|4 MHz ≈ 3.5 Ω, C = 11.37 nF, |Z|40 MHz ≈ 2 Ω,
|Z|200 MHz = 12 Ω and L = 9.55 nH.

Fig. 6: Impedance curve of a coil with 6 winding turns on a ceramic former ∅ 6 mm
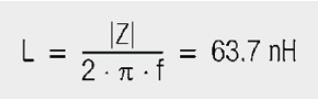
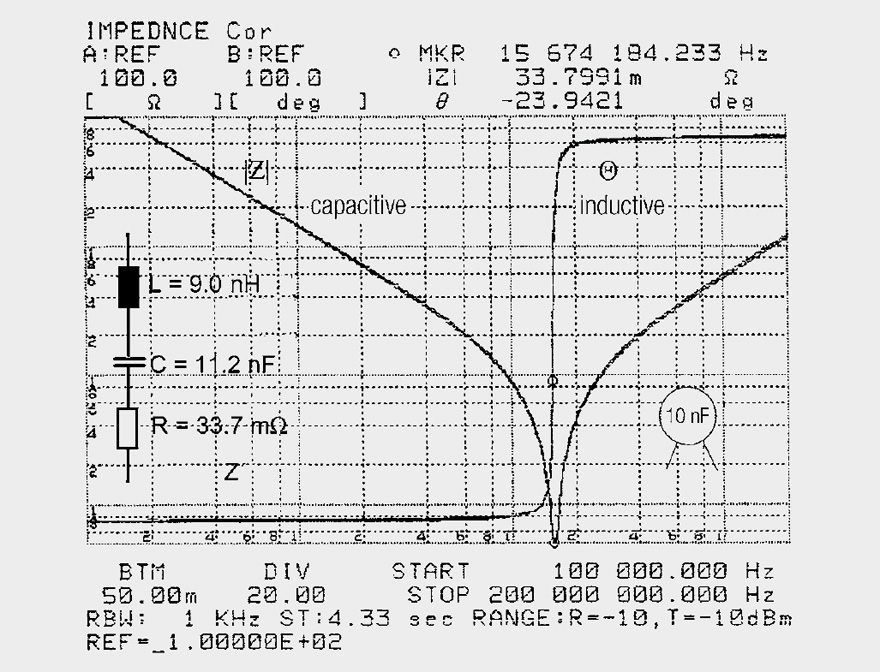
Fig. 7: Impedance curve of a 10 nF ceramic capacitor with approx. 5 mm long connecting legs
The series resistance was 33.8 mΩ according to the measurement. With the correctly selected equivalent circuit (Figure 1.45), the analyzer measured R = 33.7 mΩ, C = 11.2 nF and L = 9 nH and its coinciding curve showed that there were no further parasitic equivalent circuit parameters of any significance. Whereas the coil in Figure 1.45 is still useful at 200 MHz, the capacitor
is only applicable up to 30 MHz.
One recognizes from this, how terribly important it is to consider line inductances in association with blocking processes. An example in Figure 1.46 illustrates this
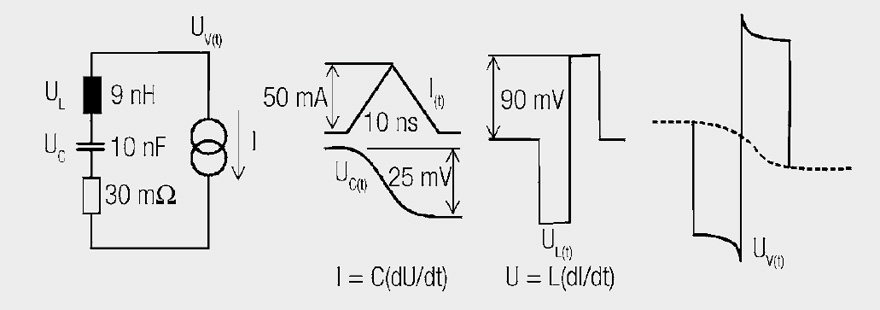
Fig. 8: The effect of a triangular pulse, as arises during the switching edge in logic circuits, on a capacitor with line inductances
If a triangular pulse reaches a “naked” capacitor without inductance, a voltage reduction of 25 mV occurs in 10 ns with a rounded falling edge. The line inductance of 9 nH alone adds a bipolar pulse with the steep edge of ±90 mV, an effect that everyone who has looked at their power supply line with an oscilloscope has observed. It is of little use to substitute 10 nF with 1 μF; if the inductance remains, the noise voltage remains. The pure change in charge in a 10 nF capacitor due to the triangular pulse leads to a change in voltage ΔU at the capacitor.
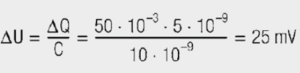
The current edges ΔI/Δt at just 9 nH generate a bipolar voltage shift of

As an example, Figure 9 shows a resonance circuit comprising a coil and capacitor in parallel with a 1 kΩ resistor. The analyzer with the structure A selected wins the equivalent circuit hands down. Other structures give rise to poor or worthless approximations. The analyzer primarily attempts to approach the phase curve. One can manually improve the parameters and arrive at new approximations.
The inductance may be determined from the measurement curve in this case. Capacitance may only be found to a limited extent. |Z|3 MHz = 4 Ω, |Z|57.6 MHz = 969 Ω, |Z|200 MHz= 24 Ω, Lp = 207 nH, Rp = 989 Ω, Cp = 36.4 pF.
The resonance condition then helps:
![]()
The analyzer results confirm the calculated values.
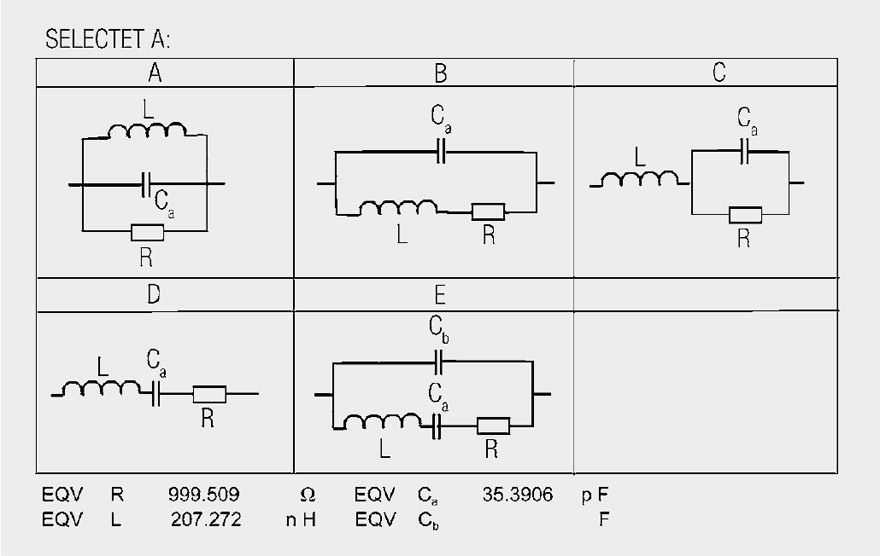
Fig. 10: Equivalent circuit types from HP4195A
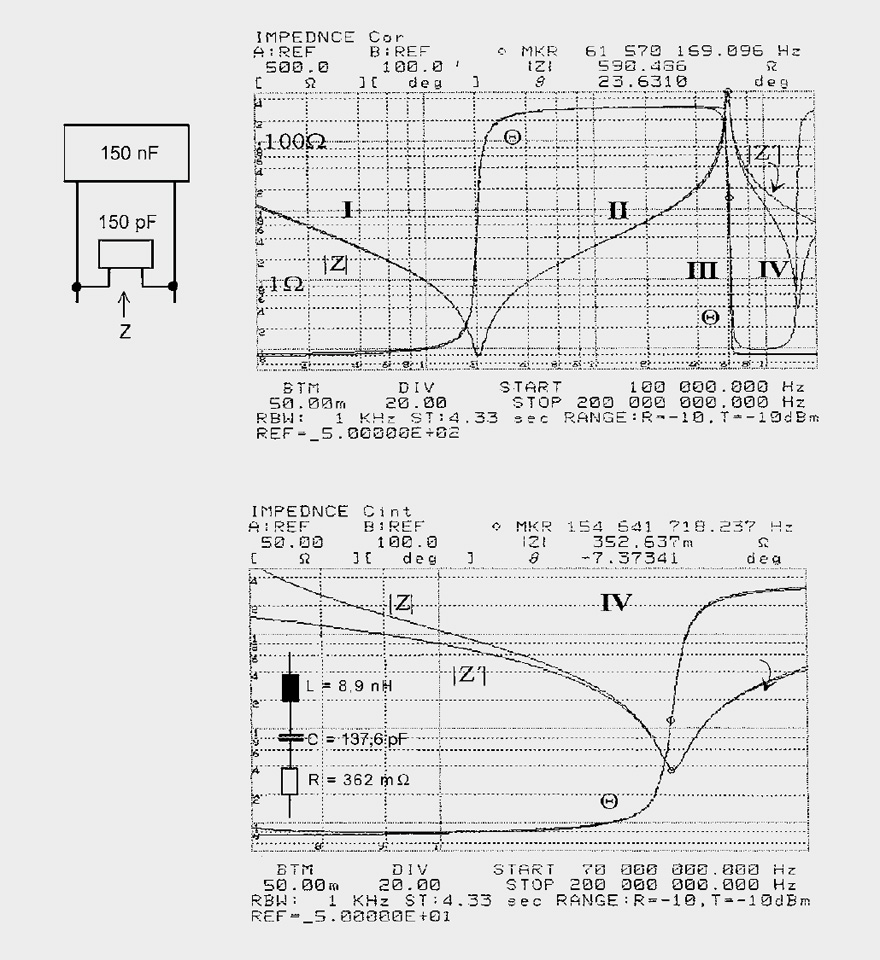
Fig. 11: Impedance curves for the parallel connection of two dissimilar capacitors (Legend of effective HF blocking)

Fig. 6: Impedance curve of a coil with 6 winding turns on a ceramic former ∅ 6 mm
Figure 11 shows the impedance curve for the parallel connection of 2 dissimilar capacitors. The larger 150 nF capacitor was supplemented with a small 150 pF capacitor to improve HF blocking. It should “balance” the disadvantage of the capacitor’s longer line to the load. The result is a resonant peak at 61.57 MHz with a Z of 590 Ω (with no load attached). Every steep pulse edge would definitely cause a long damped oscillation and the significantly reduce the usefulness of blocking.
Derivation of the equivalent circuit from the |Z| curves takes place in several steps. The phase curve Q signalizes a capacitance of up to 2 MHz (zone I). The series resonance at 2 MHz is a consequence of the approx. 4 cm long connection legs of the 150 pF capacitor. The circuit is inductive in zone II to generate a parallel resonance with 590 Ω at 60 MHz, where one can no longer
speak of blocking. From 30 MHZ–100 MHz (zone III) the impedance is greater than 100 Ω and is extremely detrimental for internal signal coupling. The 150 pF capacitor starts to play a role beyond the parallel resonance and affects a series resonance at 154 MHz. The phase curve Q is observed in zone IV.
Calculated values are
in zone I |Z|600 kHz = 2 Ω ∩ 133 nF,
in zone II |Z|20 MHz = 6.5 Ω ∩ 52 nH,
in zone III resonance 61.6 MHz Cb = 1/ω2 · L = 128.6 pF,
in zone IV resonance 154.6 MHz L – 1/ω2 · Cb = 8.25 nH
The equivalent circuit is obtained
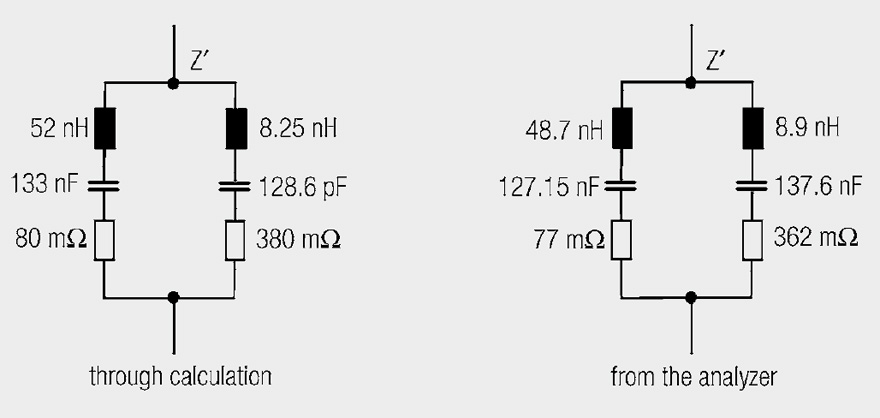
Fig. 12: Equivalent circuit of two parallel connected capacitors
Author:
EPCI | Bringing Passive Professionals Together